Frekvence zvuku v odměrném válci
Použité senzory: Mikrofon
Kategorie: Akustika
Potřeby: Odměrný válec (např. 100 ml), nebo jiná nádoba s válcovitým, úzkým tvarem; mobilní telefon s aplikací Phyphox, vodovodní kohoutek, popř konvice na vodu
Postup
Odměrný válec dejte pod vodovodní kohoutek (popř. ho postavte na stůl, pokud nemáte vodovodní kohoutek dostatečně vysoko. Otevřete aplikaci Phyphox (Obr. 1) a v ní vyberte pokus s názvem "Zvukové spektrum". Umístěte mikrofon telefonu do blízkosti hrdla odměrného válce tak, aby zachytil zvuky co nejlépe, s minimem rušivých vlivů z okolí. Přejděte na záložku "Historie". V té se nám zobrazuje časový vývoj spekter. Zapněte nahrávání pomocí tlačítka "Play" v horním pravém rohu.
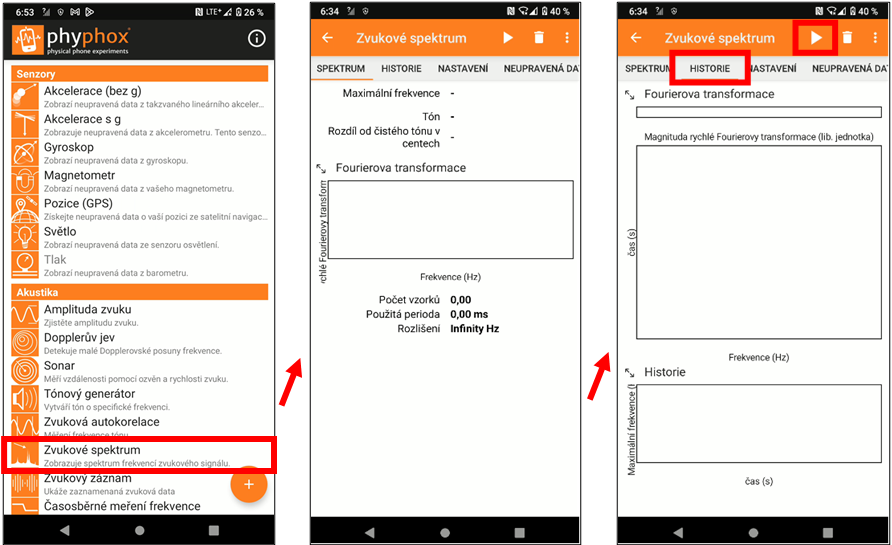
Obrázek 1. Nastavení v aplikaci Phyphox.
Pusťte tenký proud vody a konstantně ji přilévejte do sklenice (Obr. 2). Pokud máte moc nízký kohoutek a používáte konvici, je to složitější, protože kohoutkem si můžete nastavit konstantní tok vody. Pokud požíváte na přilévání konvici, musíte se o konstantní tok co nejvíce snažit. Aplikace by měla zobrazit frekvenční spektra v závislosti na čase (Obr. 3). Sledujte nejvýraznější frekvenci (rezonanční frekvenci) a jak se mění s časem (neboli s výškou hladiny vody).
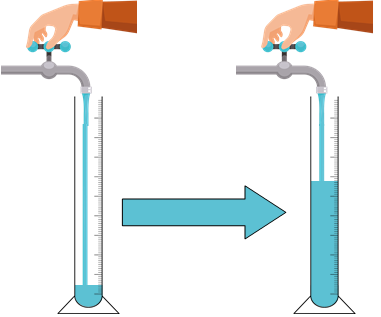
Obrázek 2. Schéma experimentu.
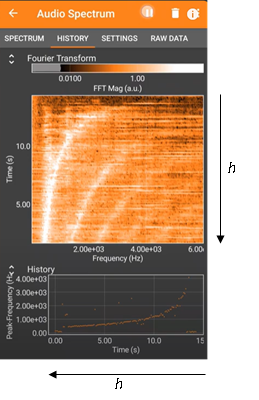
Obrázek 3. Výsledný graf.
Vysvětlení fyzikálních principů
Rezonanční frekvence se mění podle toho, jak se mění výška vzduchového sloupce nad vodou. V trubici s jedním uzavřeným koncem (jako je naše sklenice s vodou) se na uzavřeném konci (u hladiny vody) tvoří uzel (minimální amplituda) a na otevřeném konci kmitna (maximální amplituda). Tudíž nejdelší vlna má vlnovou délku čtyřikrát větší, než je výška vzduchového sloupce nad hladinou vody, druhá nejdelší vlnová délka je 4/3 výšky vzduchového sloupce nad hladinou vody atd., viz Obr. 4. Protože frekvenci můžeme vypočítat jako f = c / λ (kde c je rychlost zvuku a λ je vlnová délka), máme pro různé vlnové délky různé frekvence. To nám vysvětluje, proč na 2D grafu vidíme několik hlavních frekvencí (jedná se o tzv. vyšší harmonické).
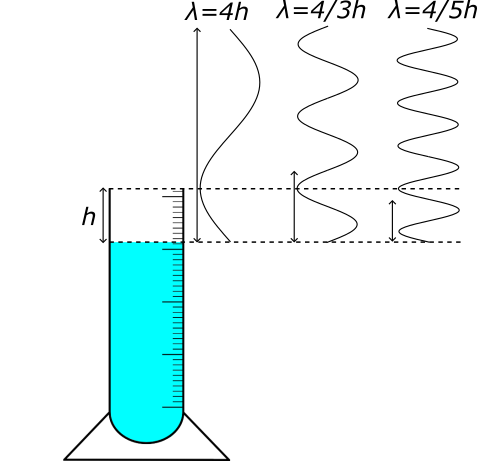
Obrázek 4. Vlnová délka v závislosti na výšce h.
Proč se ale frekvence s časem mění? Jak jsme již psali, frekvenci můžeme vypočítat jako
\[ f = \frac{c}{\lambda} \]
kde c je rychlost zvuku a λ je vlnová délka. Výška sloupce nám ale ovlivňuje délku vlny, jak je vidět z Obr. 4. Pokud dosadíme za tyto vlnové délky do předchozího vzorce, dostaneme
\[ f_0 = \frac{c}{4h} \]
\[ f_1 = \frac{3c}{4h} \]
\[ f_2 = \frac{5c}{4h} \]
\[ \dots \]
\[ f_n = \frac{(2n+1)c}{4h} \]
Jak výška vzduchového sloupce s časem klesá, stoupá nám frekvence zvuku.
Poznámky
Jaké další aplikace má rezonance v reálném životě (hudební nástroje, akustika místností)?
Demonstrační videa (v angličtině a němčině):
https://www.youtube.com/watch?v=M-FRbteXmyk
https://www.youtube.com/watch?v=cWG-noA3d_E